O Método dos Elementos Finitos: uma introdução
O ano era 1901, iniciava-se o século XX e com ele as bases para o que viria a ser conhecido posteriormente como o Método dos Elementos Finitos. De um lado, a indústria aeroespacial em busca de resolver problemas estruturais complexos. Do outro, mas talvez em sintonia, acadêmicos de engenharia estrutural debruçados sobre a possibilidade de expandir os horizontes da análise matricial de estruturas.
Assim, em torno da década de 50 o Método dos Elementos Finitos começou a ser utilizado na indústria, e em 1960 R.W. Clough de Berkley usou pela primeira vez o termo Finite Element em uma publicação. Não deixando o mérito apenas para Clough, a literatura, e particularmente os alemães, afirma que o professor J.H. Argyris (alemão) atuou ativamente nesse período no desenvolvimento do método.
Como se não fosse o bastante, matemáticos também buscam seu lugar ao sol nessa criação. Há evidências de que na década de 40 o grande matemático Courant já teria publicado um artigo onde ele resolveu um problema de vibrações utilizando elementos Finitos triangulares (sem nomeação do método). E não para por aí. Se formos mais fundo veremos os nomes Jhon William Strutt, Walther Ritz, Boris Galerkin, Hrennikoff, entre outros que contribuíram de alguma forma para o método desde o início do século XX.
Após essa introdução histórica com alta densidade de protagonistas, vamos caminhar cuidadosamente em direção ao entendimento do método sob a luz da matemática e da engenharia.
O que é o Método dos Elementos Finitos e qual a sua utilidade
À princípio, vou ser evasivo no que diz respeito à definição do Método dos Elementos Finitos e de suas aplicações. Dada a grandeza e generalidade do método, não vou me comprometer a limitá-lo a uma gama de problemas de engenharia atuais. As pesquisas podem revelar futuramente que ele é mais poderoso do que já temos considerado. Dessa forma, recorrendo à matemática, me sinto confortável apenas em defini-lo como um método aproximado de solução de equações diferenciais parciais através da minimização de funcionais.
Desculpe-me pela pretensão expressa no título deste tópico, mas vou ficar por aqui com a definição. Acredito fortemente que seja mais didático que você entenda por si só do que se trata o método e qual a sua utilidade através do desenvolvimento que será apresentado abaixo. Um pequeno alerta que faço, porém, é que aqui nos concentraremos em apenas apresentar uma introdução ao método. Portanto, ao final da leitura, saiba que o Método dos Elementos Finitos é/pode isso e muito mais.
Primeiros passos no Método dos elementos Finitos
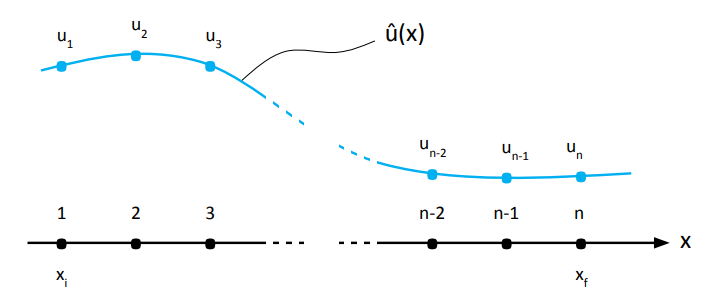
Vamos iniciar com algo simples. Proponhamos solucionar uma equação diferencial unidirecional. Esse problema terá, além da equação, um domínio no qual ela é válida e valores para a função ou sua derivada no contorno do domínio, caracterizando, dessa forma, um problema clássico de valor de contorno unidimensional. Para aplicação do MEF (Método dos Elementos Finitos) ou FEM em inglês (Finite Element Method), não é necessário que o problema tenha solução analítica. Porém, para efeito de verificação dos resultados obtidos através do método, escolheremos um caso que possua solução analítica. Dito isso, abaixo segue a expressão que, em linguagem matemática, resume todo o texto desenvolvido até aqui neste tópico.
(1) ![Rendered by QuickLaTeX.com \begin{gather*} \frac{d^{2}u}{dx^{2}}+f(x)=0 \hspace{10} em\hspace{2} \Gamma \\ \\ u(x_{i})= \={u}\hspace{5}(condição\hspace{2}de\hspace{2}contorno\hspace{2}essencial) \\ \\ \frac{du}{dx}(x_{f})=\alpha \hspace{5}(condição\hspace{2}de\hspace{2}contorno\hspace{2}natural) \\ \\ \Gamma = [x_{i}, x_{f}] \end{gather*}](https://oengenheirovirtual.com.br/blog/wp-content/ql-cache/quicklatex.com-b97fc63fa176349ac8d6134a8b585624_l3.png)
Obs.: A ideia por trás dos termos essencial e natural das condições de contorno será revelada no decorrer da leitura.
O Método dos Elementos Finitos nos permitirá obter uma função ![]() que aproxima a função
que aproxima a função ![]() . Abaixo serão apresentadas as etapas necessárias para isso.
. Abaixo serão apresentadas as etapas necessárias para isso.
Obtenção da formulação fraca do problema
A equação original (1) representa a formulação forte do problema. Essa formulação é caracterizada por equações de governo, normalmente diferenciais, e condições de contorno que exigem uma solução contínua (suave). Em contraste, a formulação fraca, com o objetivo de simplificar o problema, faz concessões no que diz respeito à condição de continuidade da solução, possuindo exigências de continuidade mais fracas. Em suma, a formulação fraca de um problema é a forma integral equivalente de sua formulação forte. Obter a formulação fraca da equação (1) será o nosso desafio dessa etapa.
Utilizaremos o método dos resíduos ponderados para obter a forma fraca da nossa equação diferencial. Há outras possibilidades de se obter a forma fraca de equações diferenciais, porém, esse método é o mais genérico entre os seus pares.
Sem delongas, então, integremos a nossa equação “forte” ao longo de todo o seu domínio.
(2) ![]()
Bom, temos agora o problema inicial na forma de uma integral. Mas é equivalente? Vamos analisar: a equação 1 exige que todo o termo dentro da integral acima valha zero ao longo de todo o domínio. Ao integrarmos esse termo e forçarmos o resultado zero não necessariamente garantimos que ele valerá zero ao longo de todo o domínio. Basta pensar numa equação hipotética h(x) com o seguinte gráfico:
![Gráfico de função no intervalo [0, 1] com equilíbrio entre área positiva (acima do gráfico) e negativa (abaixo do gráfico)](https://oengenheirovirtual.com.br/blog/wp-content/uploads/2023/02/hx-1-300x125.png)
Pela antissimetria do gráfico no intervalo ![]() fica óbvio que o fato de ser verdade que
fica óbvio que o fato de ser verdade que
(3) ![]()
Não implica em ![]() em
em ![]() .
.
Então, para não abrirmos espaço em nossa formulação fraca para uma solução que apresente valores diferentes da formulação forte ao longo do domínio, temos que garantir que o integrante da equação 2 seja nulo ao longo de todo o domínio, assim como na equação 1. Fazer isso não é tão difícil. Basta multiplicar o integrando por uma função qualquer. Sendo uma função qualquer, para que a equação seja satisfeita, obrigatoriamente a outra parte do produto deve ser zero. Pronto: a condição da equação 1 foi preservada. Matematicamente, temos:
(4) ![]()
Desvendando parcialmente o nome do método que estamos aplicando (resíduos ponderados), chamaremos ![]() de função de ponderação. Vamos, por conveniência, considerar essa função de ponderação pertencente à um espaço vetorial equivalente ao espaço vetorial da solução do problema. O efeito prático que usufruiremos dessa consideração é que as condições de contorno de
de função de ponderação. Vamos, por conveniência, considerar essa função de ponderação pertencente à um espaço vetorial equivalente ao espaço vetorial da solução do problema. O efeito prático que usufruiremos dessa consideração é que as condições de contorno de ![]() serão as mesmas de
serão as mesmas de ![]() . Aqui vem uma importante observação para que o entendimento não se perca. A condição de contorno essencial só será introduzida na resolução do sistema de equações final, portanto, independente do seu valor, devemos considerá-la igual a zero (para este problema:
. Aqui vem uma importante observação para que o entendimento não se perca. A condição de contorno essencial só será introduzida na resolução do sistema de equações final, portanto, independente do seu valor, devemos considerá-la igual a zero (para este problema: ![]() ). Dito isto, vamos manipular a equação 4.
). Dito isto, vamos manipular a equação 4.
Primeiro, separando a soma em duas integrais temos:
(5) ![]()
Segundo, aplicando a integração por partes na primeira integral, temos:
(6) ![]()
Sabendo que ![]() , podemos abrir o termo da esquerda, o que resulta em:
, podemos abrir o termo da esquerda, o que resulta em:
(7) ![]()
Repare que aparece aqui a condição de contorno ![]() da formulação forte do problema. O fato dela surgir naturalmente no desenvolvimento da forma fraca do problema concede a ela o nome que já conhecemos lá no início – condição de contorno natural. Podemos substituí-la na equação 7 por
da formulação forte do problema. O fato dela surgir naturalmente no desenvolvimento da forma fraca do problema concede a ela o nome que já conhecemos lá no início – condição de contorno natural. Podemos substituí-la na equação 7 por ![]() , bem como podemos substituir
, bem como podemos substituir ![]() por
por ![]() , que (atenção!) será zero, pois o valor de fato (
, que (atenção!) será zero, pois o valor de fato (![]() ) será considerado na equação final conforme já discutimos. Com isso, e reorganizando a equação, apresento a forma fraca do nosso problema.
) será considerado na equação final conforme já discutimos. Com isso, e reorganizando a equação, apresento a forma fraca do nosso problema.
(8) ![]()
Aproximação por elementos finitos
Vamos agora subdividir o domínio do problema em ![]() elementos finitos e, consequentemente,
elementos finitos e, consequentemente, ![]() pontos nodais.
pontos nodais.

Então, a solução do problema por elementos finitos consiste em se obter coeficiente constantes (![]() ) para cada um dos
) para cada um dos ![]() nós resultantes da discretização do domínio e, posteriormente, interpolá-los ao longo de todo o domínio utilizando funções de interpolação (
nós resultantes da discretização do domínio e, posteriormente, interpolá-los ao longo de todo o domínio utilizando funções de interpolação (![]() ).
).
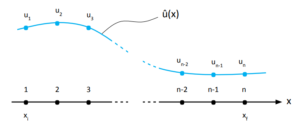
Matematicamente, a aproximação final para ![]() fica da seguinte forma:
fica da seguinte forma:
(9) 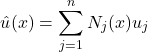
A função de interpolação deverá ser escolhida, e os coeficientes constantes serão obtidos como solução do problema em sua forma fraca (8). Veremos a parte de obtenção dos coeficientes mais adiante. Por agora, nos concentremos em entender as tão importantes funções de interpolação.
Definição das funções de interpolação
Expandindo a equação 9, temos a seguinte expressão:
(10) ![]()
Essa expressão “aberta” nos ajudará na análise que se seguirá. Observando o gráfico da figura acima vemos que no nó a função de aproximação ![]() é igual à constante
é igual à constante ![]() associada àquele nó.
associada àquele nó.
(11) 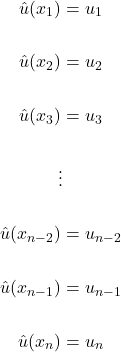
Note que para isso ocorrer é necessário que
(12) 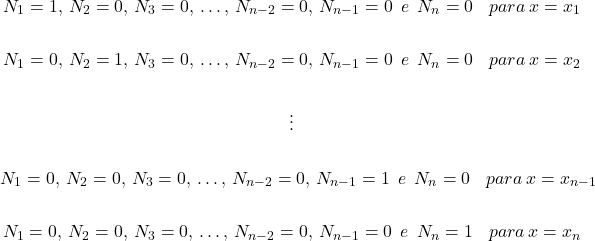
Em palavras significa dizer que a função de interpolação do nó ![]() (
(![]() ) valerá 1 no nó
) valerá 1 no nó ![]() e zero nos demais nós. Simples, não? Vejamos um exemplo: a função de interpolação linear para o nó 2.
e zero nos demais nós. Simples, não? Vejamos um exemplo: a função de interpolação linear para o nó 2.
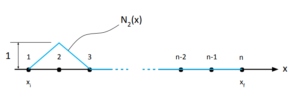
Em diversas aplicações do Método dos Elementos Finitos são utilizadas funções de interpolação lineares. Portanto, nos limitaremos a elas neste artigo. As equações que reproduzem o que está exemplificado na imagem acima estão apresentadas abaixo.
(13) 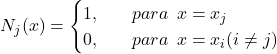
(14) 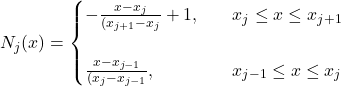
Aplicando a ideia central do Método dos Elementos Finitos
Vamos agora desvendar por completo o método dos resíduos ponderados introduzido anteriormente. Já entendemos a ponderação, basta agora compreender a ideia de resíduo. Temos discorrido bastante sobre a função ![]() que se propõe a aproximar a solução do nosso problema. Vamos agora usá-la na formulação forte do problema (Equação 1). Considerando que ela não é exatamente a função
que se propõe a aproximar a solução do nosso problema. Vamos agora usá-la na formulação forte do problema (Equação 1). Considerando que ela não é exatamente a função ![]() (digo considerando, pois em alguns casos a solução aproximada pode ser igual à solução exata), no lado direito da equação surgirá um valor diferente de zero. Esse valor, representado por
(digo considerando, pois em alguns casos a solução aproximada pode ser igual à solução exata), no lado direito da equação surgirá um valor diferente de zero. Esse valor, representado por ![]() , é chamado de resíduo. Temos a seguinte equação então:
, é chamado de resíduo. Temos a seguinte equação então:
(15) ![]()
Vamos agora exigir que esse erro seja zero. Mas não na formulação forte (senão caímos no mesmo problema inicial), e sim na formulação fraca. Então, relembrando o que desenvolvemos no tópico onde discorremos sobre a obtenção da formulação fraca, teríamos:
(16) ![]()
Que pode ser escrita em termos da função de aproximação simplesmente trocando ![]() pelo lado esquerdo da equação 15.
pelo lado esquerdo da equação 15.
(17) ![]()
E, por analogia com o que já foi visto, sabemos que se desenvolvermos essa equação chagaremos na forma fraca apresentada abaixo.
(18) ![]()
Já definimos também que ![]() pode ser aproximado por:
pode ser aproximado por:
(19) 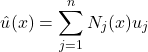
Falta-nos agora definir a função qualquer ![]() para prosseguirmos com o desenvolvimento do problema. Seguindo o mesmo princípio utilizado para a função objetivo (
para prosseguirmos com o desenvolvimento do problema. Seguindo o mesmo princípio utilizado para a função objetivo (![]() ), vamos utilizar uma aproximação para a função peso. Além disso, nos apropriando de um método largamente conhecido criado por Galerkin, e nomeado com seu próprio nome (Método de Galerkin), vamos fazer a aproximação da função peso com as mesmas funções de interpolação utilizadas para aproximar a função
), vamos utilizar uma aproximação para a função peso. Além disso, nos apropriando de um método largamente conhecido criado por Galerkin, e nomeado com seu próprio nome (Método de Galerkin), vamos fazer a aproximação da função peso com as mesmas funções de interpolação utilizadas para aproximar a função ![]() . Dessa forma, temos:
. Dessa forma, temos:
(20) ![]()
Enfim, podemos aplicar essas aproximações para ![]() e
e ![]() na formulação fraca e prosseguir o desenvolvimento da solução aproximada com elementos finitos.
na formulação fraca e prosseguir o desenvolvimento da solução aproximada com elementos finitos.
Formulação discreta do problema
Com o esforço aplicado até aqui, temos a nossa proposta de solução do problema no seguinte estágio:
(21) ![]()
Onde
(22) 
Injetando as equações das aproximações dentro da formulação fraca (21), vem:
(23) 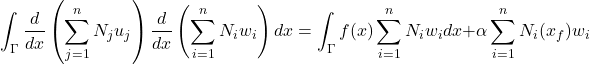
Focando primeiro no lado esquerdo da equação acima, aplicaremos a seguinte sequência de manipulação:
- Lançando mão da propriedade da derivada que diz que a derivada da soma é igual a soma das derivadas, o operador de derivada pode ser transportado para dentro do somatório.
(24) 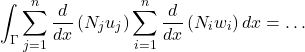
- Recordando que os coeficientes
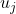 e
e 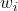 são constantes, eles podem sair da derivada.
são constantes, eles podem sair da derivada.
(25) 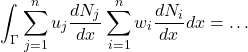
- Pelo mesmo motivo anterior, os coeficientes podem ainda ser enviados para fora da integral. Nesse caso, os somatórios devem ir juntos. E isso pode ser realizado sem problemas, pois há a propriedade das integrais que garante que a integral da soma é igual a soma das integrais.
(26) 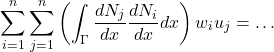
Vamos agora ao lado direito da equação. Além de ser mais simples, com a experiência obtida na manipulação do termo do lado esquerdo da equação, sinto adequado apresentar diretamente o resultado final, evitando ser prolixo.
(27) ![]()
No geral, então, temos até o momento:
(28) 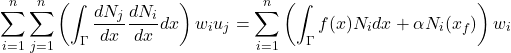
Sinto necessidade nesse momento de recordá-lo de que estamos buscando pelos valores dos coeficientes ![]() (que são as aproximações para
(que são as aproximações para ![]() nos nós) para, então, obtermos a aproximação por elementos finitos
nos nós) para, então, obtermos a aproximação por elementos finitos ![]() fazendo
fazendo ![]() . Devo lembrá-lo também de que
. Devo lembrá-lo também de que ![]() e
e ![]() são as funções de interpolação que nós devemos escolher, logo não são incógnitas.
são as funções de interpolação que nós devemos escolher, logo não são incógnitas. ![]() e
e ![]() são dados do problema e
são dados do problema e ![]() são coeficientes de ponderação arbitrários. Em resumo, as incógnitas do problema acima são os
são coeficientes de ponderação arbitrários. Em resumo, as incógnitas do problema acima são os ![]() coeficientes
coeficientes ![]() . Com isso esclarecido, simplificaremos a representação dos termos que não são incógnitas que se encontram dentro dos parênteses substituindo-os pelas letras
. Com isso esclarecido, simplificaremos a representação dos termos que não são incógnitas que se encontram dentro dos parênteses substituindo-os pelas letras ![]() e
e ![]() .
.
(29) 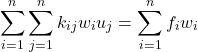
Bem melhor, não acha? Repare que o ![]() recebe tanto o índice
recebe tanto o índice ![]() quanto o índice
quanto o índice ![]() dado que o termo que ele representa depende dos dois índices. Vamos agora “abrir” esses somatórios. Pelo motivo que será desvendado mais adiante, farei isso em um formato especial como segue.
dado que o termo que ele representa depende dos dois índices. Vamos agora “abrir” esses somatórios. Pelo motivo que será desvendado mais adiante, farei isso em um formato especial como segue.
(30) 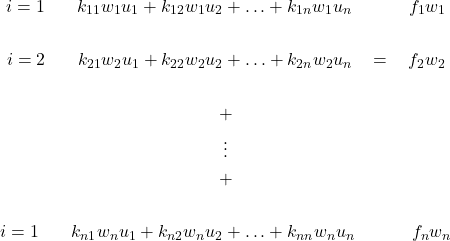
Subtraindo os termos que se encontram no lado direito em toda a equação e colocando os coeficientes ![]() em evidência, temos:
em evidência, temos:
(31) 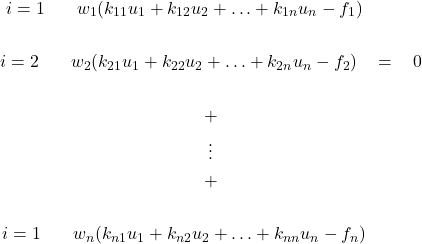
A solução trivial onde todos os coeficientes são nulos não nos interessa, pois permitiria qualquer solução para o problema. Então, necessariamente os termos entre os parênteses devem ser nulos. Com isso, temos o seguinte sistema de ![]() equações.
equações.
(32) 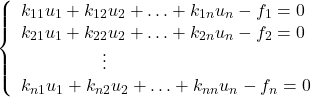
Em resumo, o sistema final de equações do Método de Elementos Finitos para o problema será:
(33) 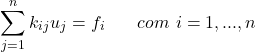
Onde
(34) 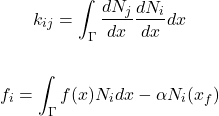
Temos ![]() equações para
equações para ![]() incógnitas. Mas essas equações são linearmente independentes? A resposta é: nem todas. No caso desse problema duas das equações são LD entre si. Mas não há motivo para preocupação, pois na verdade não temos
incógnitas. Mas essas equações são linearmente independentes? A resposta é: nem todas. No caso desse problema duas das equações são LD entre si. Mas não há motivo para preocupação, pois na verdade não temos ![]() incógnitas e sim
incógnitas e sim ![]() . O valor do coeficiente
. O valor do coeficiente ![]() em
em ![]() é igual a
é igual a ![]() . Essa é a condição de contorno essencial do nosso problema (aliás, por isso que ela recebe esse nome). Com o número de incógnitas reduzido em 1, é aceitável que duas das equações sejam LD entre si sem prejuízo à resolução do sistema.
. Essa é a condição de contorno essencial do nosso problema (aliás, por isso que ela recebe esse nome). Com o número de incógnitas reduzido em 1, é aceitável que duas das equações sejam LD entre si sem prejuízo à resolução do sistema.
Vamos agora pôr em prática toda essa teoria aprendida.
Resolução de uma equação diferencial utilizando o Método dos Elementos Finitos
Vamos resolver a seguinte equação diferencial:
(35) ![Rendered by QuickLaTeX.com \begin{gather*} \frac{d^{2}u}{dx^{2}}+f(x)=0 \hspace{10} em\hspace{2} \Gamma \\ \\ u(0)= 1\\ \\ \frac{du}{dx}(1)=\alpha = 0 \\ \\ \Gamma = [0, 1] \\ \\ f(x) = 2 \end{gather*}](https://oengenheirovirtual.com.br/blog/wp-content/ql-cache/quicklatex.com-db3128b552734c7792d0477b53b46918_l3.png)
Obtenção da forma fraca do problema
Como essa equação é similar à equação geral que foi utilizada nos tópicos anteriores, podemos obter a forma fraca do problema simplesmente substituindo ![]() ,
, ![]() e
e ![]() da equação 8 pelos valores deste problema.
da equação 8 pelos valores deste problema.
(36) ![]()
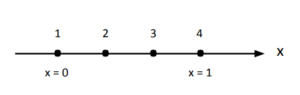
Discretização do domínio em elementos finitos
O domínio, nesse caso linear, será dividido em 3 elementos finitos. Isso resultará em 4 nós, enumerados conforme a figura a seguir.
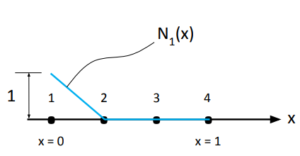
Definição das funções de interpolação
Para cada um dos nós teremos uma função de interpolação. Elas serão, por escolha, lineares. Abaixo estão apresentadas as equações de interpolação de cada nó e as respectivas representações gráficas delas.
(37) ![]()
(38) 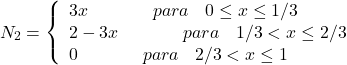
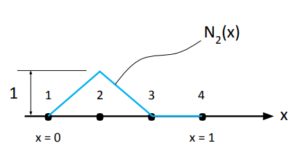
(39) 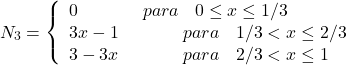
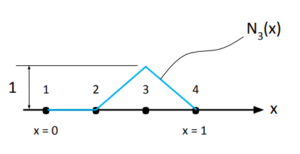
(40) ![]()
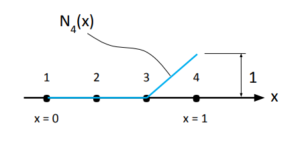
Repare que seguimos fielmente a regra das funções de interpolação: ter valor 1 no nó ao qual ela diz respeito e valer 0 nos demais nós.
Montagem do sistema algébrico de elementos finitos
Construiremos o sistema algébrico para este problema conforme a Equação 33 já apresentada. Para isso, é necessário calcular os valores de ![]() e
e ![]() . Como o problema que estamos resolvendo é similar ao problema considerado no desenvolvimento teórico, esses valores podem ser obtidos pelas expressões da Equação 34, substituindo apenas os valores de
. Como o problema que estamos resolvendo é similar ao problema considerado no desenvolvimento teórico, esses valores podem ser obtidos pelas expressões da Equação 34, substituindo apenas os valores de ![]() e
e ![]() . Temos, então, a seguinte sequência de cálculos:
. Temos, então, a seguinte sequência de cálculos:
(41) ![]()
(42) 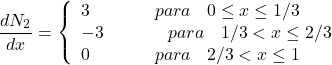
(43) 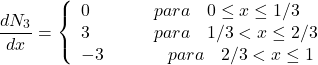
(44) ![]()
(45) ![]()
(46) ![]()
(47) ![]()
(48) ![]()
(49) ![]()
(50) ![]()
(51) ![]()
(52) ![]()
(53) ![]()
(54) ![]()
(55) ![]()
(56) ![]()
(57) ![]()
(58) ![]()
(59) ![]()
(60) ![]()
Nesse momento preciso destacar duas características dos coeficientes ![]() que podem ser extraídas dessa sequência árdua de cálculo de integrais presenciada acima.
que podem ser extraídas dessa sequência árdua de cálculo de integrais presenciada acima.
- O valor de
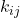 sempre será zero se os nós
sempre será zero se os nós 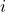 e
e 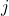 não estiverem conectados por um elemento finito comum; e
não estiverem conectados por um elemento finito comum; e - Os valores
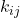 são simétricos, isto é,
são simétricos, isto é, 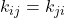 .
.
Saber isso anteriormente nos teria poupado algumas integrações. Mas assim é melhor, pois o leitor pôde visualizar essas duas afirmações sendo validadas.
Vamos agora calcular os valores de ![]() .
.
(61) ![]()
(62) ![]()
(63) ![]()
(64) ![]()
Assim, já podemos montar o sistema de equações de elementos finitos.
(65) 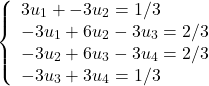
Que, em formato matricial, se apresenta da seguinte forma:
(66) 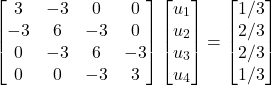
Resolução do sistema de equações de elementos finitos
Se tentarmos resolver o sistema de equações final que obtivemos para o nosso exemplo não teremos êxito, pois o sistema obtido não tem solução. Precisamos utilizar a condição de contorno essencial (![]() ) para reduzir o número de incógnitas. O sistema então passa a ser:
) para reduzir o número de incógnitas. O sistema então passa a ser:
(67) 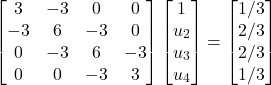
Que pode ser simplificado para:
(68) 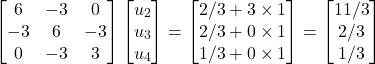
Resolvendo-o, temos o seguinte resultado:
(69) ![]()
Pronto! Agora sabemos os valores da função ![]() nos nós resultantes da discretização em elementos finitos que fizemos no domínio do problema. Vamos agora gerar a função de aproximação
nos nós resultantes da discretização em elementos finitos que fizemos no domínio do problema. Vamos agora gerar a função de aproximação ![]() .
.
Função de aproximação de elementos finitos
Lembrando o que já foi visto, a função de aproximação se apresenta da seguinte forma:
(70) 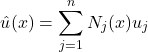
No problema em questão será, então:
(71) ![]()
Substituindo as funções de aproximação que foram definidas para o problema, tem-se por fim:
(72) 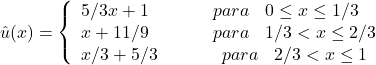
Sabendo que a solução exata para esse problema é a equação
(73) ![]()
Podemos plotar o gráfico da curva da aproximação de elementos finitos sobre o gráfico da curva exata. Fazendo isso obtemos:
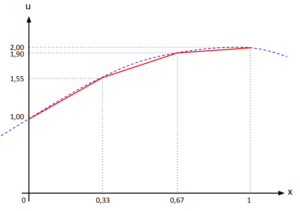
Acho que, observando o gráfico acima, o leitor há de concordar que conseguimos aproximar a solução do problema utilizando o Método dos Elementos Finitos. E se usássemos funções de interpolação quadráticas, como seria o resultado? Como a solução exata desse problema é quadrática, a resposta é que encontraremos exatamente a solução do problema. Com essa observação final, fecho esse primeiro exemplo de aplicação do método de elementos finitos.
Resolução do problema da barra carregada axialmente utilizando o Método dos Elementos Finitos
Vamos agora a um exemplo específico de engenharia: obter os deslocamentos ao longo de uma barra carregada axialmente utilizando elementos finitos. Seguindo a notação que vem sendo utilizada, a incógnita do problema (campo de deslocamento), será chamada de ![]() .
.
Entrando em mais detalhes, o problema consiste em uma barra de comprimento ![]() com geometria de seção constante ao longo do comprimento. Ela está engastada em uma extremidade e livre na outra e possui um carregamento distribuído
com geometria de seção constante ao longo do comprimento. Ela está engastada em uma extremidade e livre na outra e possui um carregamento distribuído ![]() ao longo do comprimento e outro pontual
ao longo do comprimento e outro pontual ![]() na extremidade livre, ambos na direção axial da barra. O esquema abaixo ilustra o problema.
na extremidade livre, ambos na direção axial da barra. O esquema abaixo ilustra o problema.
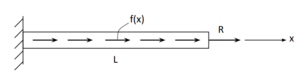
Vamos às etapas do método de elementos finitos. Diferentemente do caso anterior, aqui iniciaremos um passo atrás. Desenvolveremos a formulação forte do problema.
Desenvolvimento da formulação forte do problema
Consideremos um elemento infinitesimal de comprimento ![]() da barra. Atuará nele a força externa
da barra. Atuará nele a força externa ![]() e as forças internas (
e as forças internas (![]() ) em cada uma de suas extremidades.
) em cada uma de suas extremidades.
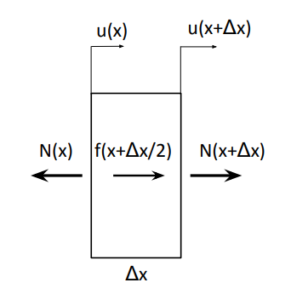
Para que o elemento infinitesimal esteja em equilíbrio, é necessário que a soma de todas as forças atuando sobre ele seja igual a zero. Assim,
(74) ![]()
Dividindo todos os termos por ![]() , temos:
, temos:
(75) ![]()
Fazendo o limite quando ![]() tende a zero, teremos o primeiro termo do lado esquerdo como sendo a própria definição de derivada e no segundo termo a parcela
tende a zero, teremos o primeiro termo do lado esquerdo como sendo a própria definição de derivada e no segundo termo a parcela ![]() poderá ser desprezada. Disso resulta:
poderá ser desprezada. Disso resulta:
(76) ![]()
Agora vamos definir o ![]() , a força interna. Sabe-se pela Lei de Hooke que
, a força interna. Sabe-se pela Lei de Hooke que
(77) ![]()
E, por definição, para o elemento infinitesimal
(78) ![]()
Analogamente ao caso anterior, fazendo o limite quando ![]() tende a zero, teremos
tende a zero, teremos
(79) ![]()
Substituindo então na equação 77, obtemos:
(80) ![]()
Levando esse resultado para a equação 76, obtemos, por fim, a equação “forte” que modela o nosso problema.
(81) ![]()
Para finalizar esse tópico ainda é necessário definir as condições de contorno do problema. Como em ![]() a barra está engastada, é fácil concluir que o deslocamento nesse ponto será zero. Além disso, também é possível notar que em
a barra está engastada, é fácil concluir que o deslocamento nesse ponto será zero. Além disso, também é possível notar que em ![]() a força interna na barra (
a força interna na barra (![]() ) será igual a força
) será igual a força ![]() aplicada na extremidade da barra. Assim, podemos intuir diretamente as seguintes condições de contorno:
aplicada na extremidade da barra. Assim, podemos intuir diretamente as seguintes condições de contorno:
(82) 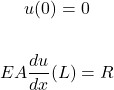
Feito! Vamos agora obter a forma fraca.
Obtenção da forma fraca do problema
Se o leitor é atento, vai perceber que a forma forte do problema da barra é análoga à forma forte do problema anterior. Com isso, por semelhança, já posso escrever direto que a forma fraca desse problema será:
(83) ![]()
Discretização do domínio em elementos finitos
O domínio será dividido em 3 elementos finitos, conforme no problema anterior. Para agilizar o processo vamos considerar o comprimento ![]() da barra como sendo 1m. Dessa forma, a discretização do domínio recairá exatamente na discretização do exemplo anterior. Como vamos considerar funções de interpolação lineares nesse exemplo, poderemos reutilizar as funções de interpolação calculadas no exemplo anterior. Como o domínio (
da barra como sendo 1m. Dessa forma, a discretização do domínio recairá exatamente na discretização do exemplo anterior. Como vamos considerar funções de interpolação lineares nesse exemplo, poderemos reutilizar as funções de interpolação calculadas no exemplo anterior. Como o domínio (![]() ) e a discretização (3 elementos finitos de tamanhos iguais) para os dois exemplos são semelhantes, as funções de interpolação lineares também serão iguais. Dessa forma, vamos direto à montagem do sistema de equações de elementos finitos.
) e a discretização (3 elementos finitos de tamanhos iguais) para os dois exemplos são semelhantes, as funções de interpolação lineares também serão iguais. Dessa forma, vamos direto à montagem do sistema de equações de elementos finitos.
Montagem do sistema algébrico de elementos finitos
Por similaridade com o exemplo anterior, as equações de elementos finitos para se definir os valores de ![]() e de
e de ![]() são as apresentadas abaixo.
são as apresentadas abaixo.
(84) 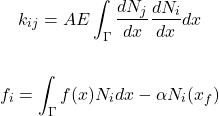
Para obter os valores de ![]() vamos adotar
vamos adotar ![]() igual a
igual a ![]() e
e ![]() igual a
igual a ![]() . Com isso, o produto
. Com isso, o produto ![]() será igual a
será igual a ![]() . Como esse fator
. Como esse fator ![]() é o único elemento que difere do exemplo anterior, para obter a matriz
é o único elemento que difere do exemplo anterior, para obter a matriz ![]() deste problema, basta então aplicar esse fator à matriz do exemplo anterior. Dessa forma, temos que:
deste problema, basta então aplicar esse fator à matriz do exemplo anterior. Dessa forma, temos que:
(85) 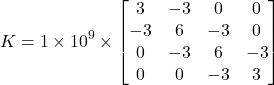
Para calcular os valores de ![]() vamos assumir que
vamos assumir que ![]() vale
vale ![]() e que
e que ![]() . Dessa forma, seguem os cálculos:
. Dessa forma, seguem os cálculos:
(86) ![]()
(87) ![]()
(88) ![]()
(89) ![]()
Assim, juntando as partes, temos o sistema de equação para o problema de elementos finitos:
(90) 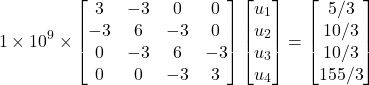
Resolução do sistema de equações de elementos finitos
O primeiro passo aqui consiste em reduzir o sistema de equações utilizando a condição de contorno essencial – ![]() . Fazendo isso, temos:
. Fazendo isso, temos:
(91) 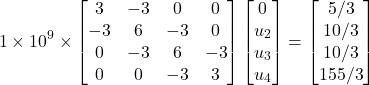
Que pode ser simplificado para:
(92) 
Resolvendo-o, temos o seguinte resultado:
(93) ![]()
Vamos agora gerar a função de aproximação por elementos finitos ![]() .
.
Função de aproximação de elementos finitos
A função de aproximação por elementos finitos desse problema será da seguinte forma:
(94) ![]()
Substituindo as funções de aproximação que foram definidas para o problema, tem-se por fim:
(95) ![Rendered by QuickLaTeX.com \begin{equation*} û(x) = \left\{ \begin{array}{ll} 5,82x \hspace{5} [10^{-8}m] \hspace{40} para \hspace{10} 0\leq x\leq 1/3\\ 0,1+5,52x \hspace{5} [10^{-8}m]\hspace{40} para \hspace{10} 1/3<x\leq 2/3 \\ 0,34+5,16x\hspace{5} [10^{-8}m] \hspace{40} para \hspace{10} 2/3<x\leq 1 \end{array}\right \end{equation*}](https://oengenheirovirtual.com.br/blog/wp-content/ql-cache/quicklatex.com-c8d278549342e6fa32ff026db86f3135_l3.png)
A solução exata para esse problema é a equação apresentada abaixo:
(96) ![]()
Se plotássemos os gráficos da função ![]() e de sua aproximação teríamos um resultado semelhante ao do exemplo anterior.
e de sua aproximação teríamos um resultado semelhante ao do exemplo anterior.
Pronto, mais um exemplo de aplicação do Método dos Elementos Finitos concluído.
Livro sobre elementos finitos
Há muitas referências de qualidade para se estudar o método dos Elementos Finitos. Dentre elas, indico o livro em língua portuguesa do Dr. Fernando Luiz B. Ribeiro, professor da disciplina de Elementos Finitos da UFRJ por décadas. Esse livro traz teoria e prática numa dosagem didaticamente confortável. Ele pode ser obtido na loja virtual da Amazon através do seguinte endereço: introdução ao Método dos Elementos Finitos.
Considerações finais sobre o Método dos Elementos Finitos
Apesar de termos atualmente uma gama de softwares especializados em análises numéricas envolvendo o Método dos Elementos Finitos, é imprescindível ter pelo menos os conhecimentos básicos do método para tomar decisões assertivas na etapa de modelagem e discretização do modelo e na etapa final de crítica aos resultados encontrados. Finalizo enfatizando dramaticamente: software de elementos finitos na mão de desconhecedores do método, apesar de toda a robustez que possa ter, será uma caixa preta que receberá números como input e devolverá números como output.