O método dos mínimos quadrados
Algumas vezes temos em posse um conjunto de dados e queremos representar o comportamento deles através de uma expressão matemática, seja para fazer projeções fora do espaço amostral dos dados, para analisar interdependência ou, até mesmo, para confirmar hipóteses. Enfim, são muitas as aplicações para isso que podem surgir através da incrível capacidade cognitiva humana.
Aproximar um conjunto de pontos por uma curva de forma que o erro seja mínimo não é uma tarefa trivial, mas é justamente isso que o Método dos Mínimos Quadrados (em inglês, Least Squares Fitting) se propõe a fazer. Veremos no detalhe como o método funciona.
Dados de entrada
Antes de tudo, é necessário definir o conjunto de dados a ser aproximado pelo Método dos Mínimos Quadrados. De forma genérica, definamos ![]() pontos no
pontos no ![]() , como mostrado na tabela abaixo.
, como mostrado na tabela abaixo.
Além disso, precisamos escolher as funções que definirão a expressão analítica de aproximação. De maneira genérica, definamos ![]() funções para a aproximação e
funções para a aproximação e ![]() respectivos coeficientes para essas funções. A expressão analítica da curva de aproximação será o somatório do produto entre o
respectivos coeficientes para essas funções. A expressão analítica da curva de aproximação será o somatório do produto entre o ![]() coeficiente e a
coeficiente e a ![]() função. Parece confuso? A equação abaixo tem o propósito de eliminar quaisquer imprecisões e confusões em minhas palavras.
função. Parece confuso? A equação abaixo tem o propósito de eliminar quaisquer imprecisões e confusões em minhas palavras.
(1) 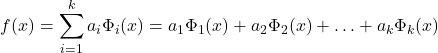
Onde:
![]() é o i-ésimo coeficiente; e
é o i-ésimo coeficiente; e
![]() é a i-ésima função.
é a i-ésima função.
Para facilitar o entendimento com relação à função de aproximação, vejamos o simples exemplo a seguir onde se deseja aproximar um conjunto de pontos utilizando um polinômio do primeiro grau. Sabe-se que um polinômio do primeiro grau genérico se escreve da seguinte maneira:
(2) ![]()
Utilizando a estrutura apresentada na Equação 1, isto nada mais é do que
(3) 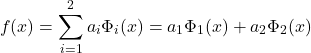
Onde:
![]() ;
;
![]() ; e
; e
![]() e
e ![]() os coeficientes a determinar.
os coeficientes a determinar.
Com isso, considera-se a parte de dados necessários para a realização da aproximação concluída. Prossigamos para a aplicação do Método dos Mínimos Quadrados sobre eles agora.
O Método dos Mínimos Quadrados (MMQ)
De maneira visual, vamos lançar os pontos da amostra no espaço cartesiano e fazer a representação da curva ![]() que usaremos na aproximação passando por entre eles.
que usaremos na aproximação passando por entre eles.
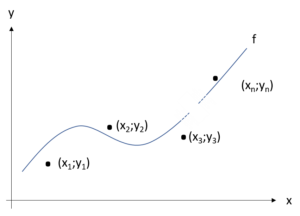
O parâmetro que mede quão boa é a aproximação realizada pela curva ![]() em relação aos pontos conhecidos é a soma dos erros em cada um dos pontos. Matematicamente, o erro no ponto j-ésimo seria:
em relação aos pontos conhecidos é a soma dos erros em cada um dos pontos. Matematicamente, o erro no ponto j-ésimo seria:
(4) ![]()
Antes de fazer a soma desse erro para todos os pontos é importante observar que, a depender da posição do ponto em relação à curva (acima ou abaixo), o sinal do erro será diferente. Da forma que foi calculado o erro, se estiver acima será negativo e se estiver abaixo será positivo. Então, para que os erros negativos não compensem os erros positivos e tenhamos um somatório total de erros falseado, adota-se o valor absoluto do erro.
Então, a soma do erro será:
(5) 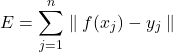
Uma vez definido o erro total do problema, basta minimizá-lo. Por questões de facilidade de manipulação matemática, ao invés de usar o valor absoluto do erro, será considerado o quadrado do erro. Minimizar o quadrado do erro é equivalente a minimizar o próprio erro, então o resultado não será afetado adotando-se essa estratégia.
O erro quadrado fica então escrito da seguinte forma:
(6) 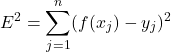
Substituindo a ![]() pela expressão definidas anteriormente, temos:
pela expressão definidas anteriormente, temos:
(7) 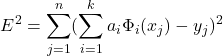
Assim, chegamos ao ponto onde a equação do erro quadrado está definida em função dos pares ![]() , que são conhecidos no problema assim como o operador
, que são conhecidos no problema assim como o operador ![]() que é aplicado ao
que é aplicado ao ![]() , e dos coeficientes
, e dos coeficientes ![]() que são as incógnitas do problema. Usando um conceito de mínimos e máximos da matemática diferencial (saiba mais), derivamos o quadrado do erro em relação a cada uma dos
que são as incógnitas do problema. Usando um conceito de mínimos e máximos da matemática diferencial (saiba mais), derivamos o quadrado do erro em relação a cada uma dos ![]() coeficientes (que são as variáveis) e igualarmos a zero, gerando assim um sistema de
coeficientes (que são as variáveis) e igualarmos a zero, gerando assim um sistema de ![]() equações. O sistema é apresentado abaixo:
equações. O sistema é apresentado abaixo:
(8) 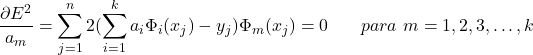
Como o sistema de equação apresenta valor nulo no lado direito, ele pode ser dividido por 2 para não termos mais o o valor 2 multiplicando o sistema. Além disso, passando o termo independente dos coeficientes ![]() para o lado direito e direito, temos:
para o lado direito e direito, temos:
(9) 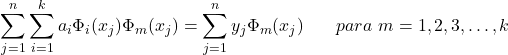
Passando para o formato matricial, então, temos a equação abaixo (se não acompanhou essa passagem, sugiro que “abra” com calma os somatórios da Equação 9).
(10) 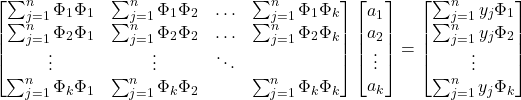
OBS.: Sabendo que ![]() . O
. O ![]() só foi omitido para simplificar a apresentação da matriz.
só foi omitido para simplificar a apresentação da matriz.
Chamando a matriz de ![]() , o vetor de coeficientes de
, o vetor de coeficientes de ![]() e o lado direito da equação
e o lado direito da equação ![]() , a equação pode ser escrita da seguinte forma:
, a equação pode ser escrita da seguinte forma:
(11) ![]()
Assim, o vetor de coeficientes, que é a incógnita do problema, pode ser isolado. Para isso, basta pré-multiplicar os dois lados da Equação 11 pela inversa de ![]() . Com isso
. Com isso ![]() do lado esquerdo resultará (por definição) na matriz identidade, que multiplicada pelo vetor
do lado esquerdo resultará (por definição) na matriz identidade, que multiplicada pelo vetor ![]() resultará no próprio vetor e o lado direito ficará conforme mostrado abaixo.
resultará no próprio vetor e o lado direito ficará conforme mostrado abaixo.
(12) ![]()
Dessa forma, do ponto de vista matemático, o problema está resolvido. No próximo tópico veremos uma abordagem prática para encontrar o vetor de coeficientes.
Abordagem prática do Método dos Mínimos Quadrados
Agora vamos por em prática o método aprendido! Como o processo será manual, faremos a aproximação para uma reta. Como sabemos (ver Equação 2), a equação da reta exige dois coeficientes a serem determinados, ![]() e
e ![]() . Associados à esses coeficientes estão as funções
. Associados à esses coeficientes estão as funções ![]() e
e ![]() .
.
Dessa forma, montando o sistema temos:
(13) ![]()
Substituindo as expressões das funções ![]() e
e ![]() , temos:
, temos:
(14) ![]()
utilizando o formato apresentado na Equação 12, onde o vetor de coeficiente está isolado, o sistema de equações passa a ser:
(15) 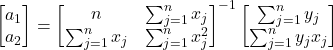
Operando a inversa da matriz ![]() , a equação passa a ser (daqui para frente os limetes do somatório serão omitidos para despoluir as equações):
, a equação passa a ser (daqui para frente os limetes do somatório serão omitidos para despoluir as equações):
(16) ![]()
Daí, podemos retirar facilmente as equações para os coeficientes em função dos ![]() pares
pares ![]() dados do problema.
dados do problema.
(17) 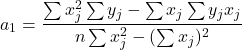
(18) ![]()
Feito! Dado um conjunto de pontos, somos capazes de obter o coeficiente angular (![]() ) e linear (
) e linear (![]() ) da reta que melhor aproxima esses pontos segundo o Método dos Mínimos Quadrados.
) da reta que melhor aproxima esses pontos segundo o Método dos Mínimos Quadrados.
Considerações finais sobre o Método dos Mínimos Quadrados
O Método dos Mínimos Quadrados é uma importante ferramenta para os mais diversos profissionais, uma vez que permite a modelagem matemática de dados experimentais. Isso é essencial, pois com modelos matemáticos os dados passam a ter maior valor para análises e previsões.

